汪道之

有人的地方就有江湖

0%

编译原理第七章-自上而下的语法分析

发表于 更新于 分类于

导语

  1. 语法分析是对高级语言的语法单位的结构进行分析
  2. 语法单位结构可以用上下文无关文法描述
  3. 下推自动机可识别上下文无关文法所描述的语法单位
  4. 上下文无关文法和下推自动机是语法分析的理论基础

引言

自上而下：从文法开始符出发，能否找到一个最左推导序列，使得S=>*w；或者从根节点S开始，能否构造一棵语法树，使得该语法树的叶节点自左至右的连接正好是w

不确定：回溯分析法
确定：递归下降分析法、预测分析法

自下而上：从w出发，能否找到一个最左规约（最右推导的逆过程）序列，逐步进行规约，直至文法的开始符号S

回溯分析法

回溯

产生回溯的原因

  1. 公共左因子

    在文法的产生式集合中，某个非终结符的多个候选式具有相同的前缀，一般，公共左因子的产生式为A→αβ1│αβ2

    采取试探的方法分析每个候选式，很可能产生回溯

  2. 左递归

    左递归的形式为
    A=>^+^ A β
    特别地
    A=> A β
    就是直接左递归

  3. ε产生式

    在具有ε的产生式中也会由于不知道匹配哪一个而产生回溯，例如

    ​ S→aAS|b
    ​ A→bAS|ε
    对符号串ab的分析

特点

  1. 不确定
  2. 试探每一种可能
  3. 不成功则回退
  4. 穷尽所有推导

缺陷

  1. 盲目
  2. 文法存在左递归则可能产生无限循环
  3. 引起时间空间的大量消耗
  4. 无法指出语法错误的确切位置

消除回溯

  1. 要么只有一个候选式可用
  2. 要么没有候选式可用

递归下降分析法

提取公共左因子

A->αβ1 |αβ2 |…|αβn |δ

改写为：

A->αB|δ

B->β1|β2 |βn

反复提取，直至所有产生式都没有公共左因子

左递归的消除（改写）

直接左递归的消除

A->Aα|β

改写为右递归形式

A->βA’

A’->αA’|ε

间接左递归的消除

A=>^+^ Aα

利用算法

  1. 将文法G的所有非终结符按任一给定顺序排列为A1 , A2 , …, An

  2. 消除可能的左递归

    1
    2
    3
    4
    5
    6
    7
    for i:=1 to n do
       begin
          for j:=1 to i-1 do        
             把形如Ai->Ajα的产生式改写为//达到Aj全都是由终结符或者j后面的非终结符开头的
                  Ai->δ1α|δ2α|...|δ3α//Aj->δ1|δ2|δ3,相当于展开Aj
          消除Ai产生式可能的直接左递归//此时Ai都是由终结符或者Ai及其以后的非终结符开头，下面消除Ai开头的直接左递归
        end

  3. 化简

递归下降分析器的构造

没有任何公共左因子，没有任何左递归，则有可能构造出不带回溯的分析程序

只有当候选式以终结符开始或最多只有一个非终结符开始的时候才可以构造出来

递归下降分析

分析程序由一组递归过程组成
每个过程对应文法的一个非终结符
对相应产生式的右部进行分析

扩充的文法

{α}表示闭包运算α*
[α]表示α的出现可有可无，即[α]=α|ε

左递归的消除：

A->x|y|Av

改写成：

A->(x|y)|{v}

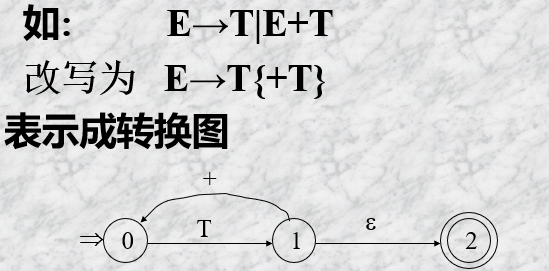
例如：

image-20210620105417192

预测分析法

  1. 表驱动

    下推栈、预测分析表、控制程序

  2. 是下推自动机的一种实现模型

预测分析过程

  1. 预测分析表：记录预测的结论
    形式：M[A,a]矩阵，A∈VN , a∈VT ∪）和当前的输入符号a（a∈VT ∪